怎么求3X3矩阵的逆矩阵

手工计算一个3x3矩阵的逆矩阵是一项繁琐的工作，但它非常有用，比如求解各种矩阵方程。

方法1传统的计算方法

1. 

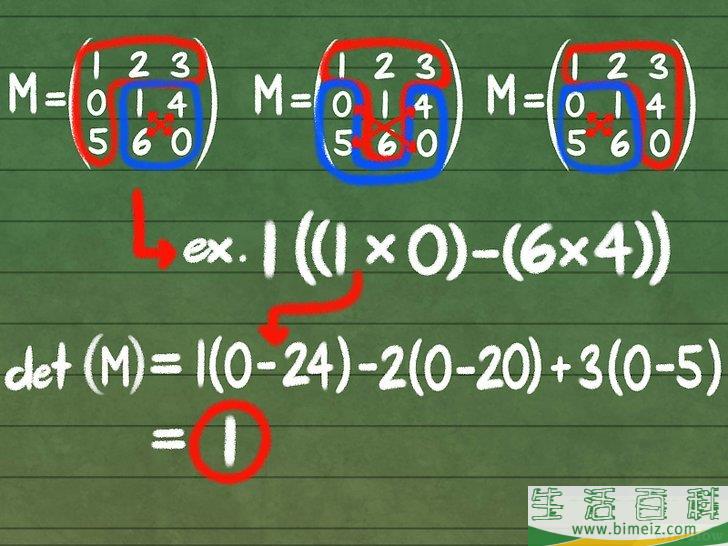
   1求出 det(M) ,也就是矩阵M的行列式的值。

   行列式的值通常显示为逆矩阵的分母值，如果行列式的值为零，说明矩阵不可逆。
2. 

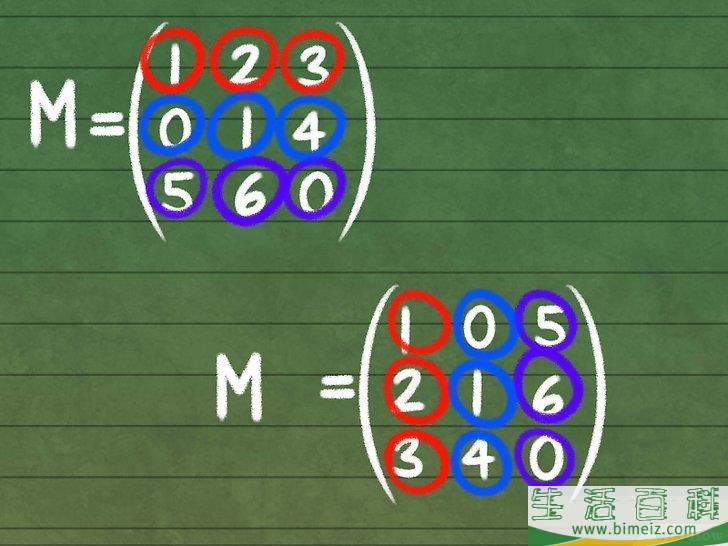
   2求出 M , 即转置矩阵。

   矩阵的转置体现在沿对角线作镜面反转，也就是将元素 (i,j) 与元素 (j,i) 互换。
3. 

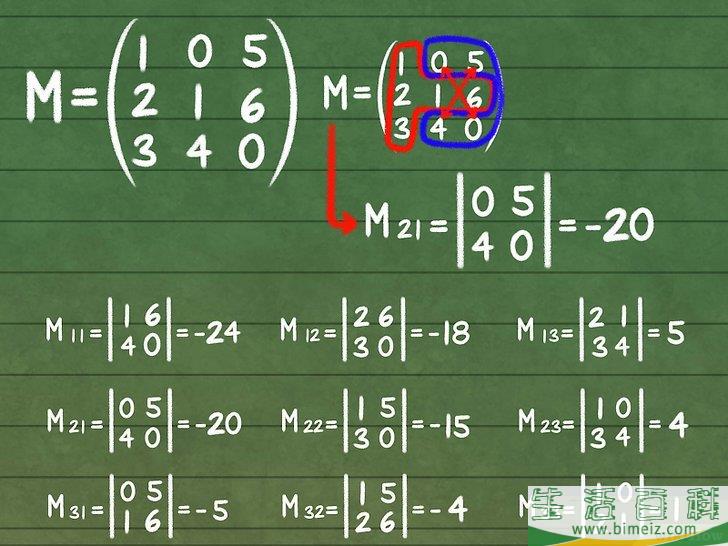
   3求出每个2X2小矩阵的行列式的值。

4. 

   4将它们表示为如图所示的辅助因子矩阵，并将每一项与显示的符号相乘。

   这样就得到了伴随矩阵（有时也称为共轭矩阵），用 Adj(M) 表示。
5. 

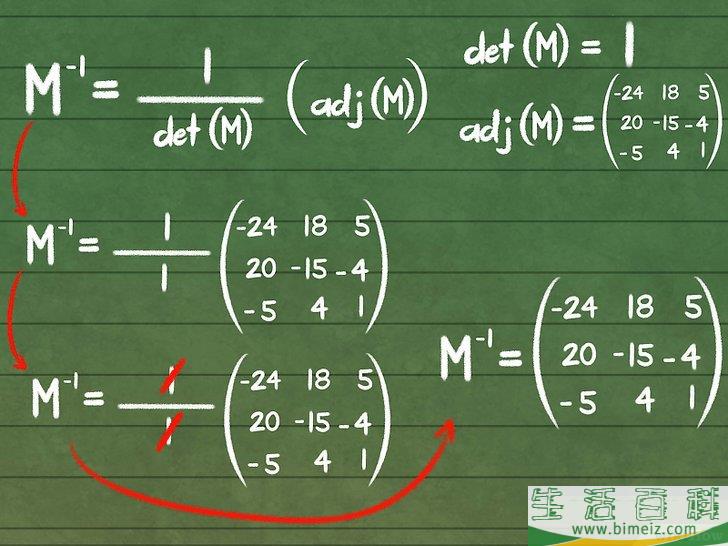
   5由前面所求出的伴随矩阵除以第一步求出的行列式的值，从而得到逆矩阵。

6. 

   6对逆矩阵转置，然后列出每个元素周围的2x2矩阵。

   检查三遍行列式的值，如果和原矩阵对应的位置的数相同，那么你求出的结果就是原矩阵的逆矩阵。使用这个方法，不需要担心符号的问题。

方法2楔积法（使用格拉斯曼代数）

1. 

   1用M表示3x3的矩阵，D 表示它的逆矩阵。

   用

   c

   _i 表示M的列向量，其中i = 0..2。
2. 2计算D =

   c

   ^

   c

   ₁ ^

   c

   ₂ ，其中'^'表示楔积。
3. 如果D 为零，那说明M没有逆矩阵。
4. 否则，M的第i 行 = (

   c

   _{(i+1) mod 3} ^

   c

   _{(i + 2) mod 3} )) / D ，其中i = 0.2

注意事项

注意，这个方法也可以应用于含变量或未知量的矩阵中，比如代数矩阵 M 和它的逆矩阵 M 。

将所有怎么求3X3矩阵的逆矩阵的方法都写下来，因为要想心算3X3矩阵的逆是极其困难的。

有些计算机程序也可以计算出矩阵的逆。最高可以求出30X30的矩阵。

伴随矩阵是辅助因子矩阵的转置，这就是为什么在第二步中我们要将矩阵转置以求出辅助因子的转置矩阵。

可以通过将 M 与 M相乘检验结果。你应该能够发现，M*M = M*M = I. I 是单位阵，其对角线上的元素都为1，其余元素全为0。否则，你可能在某一步出了错。

警告

不是所有的3X3矩阵都存在逆矩阵。如果矩阵的行列式的值为零，它就不存在逆矩阵。 (注意到在公式里我们会除以 det(M)，除数为零时是没有意义的。)

本文转自:www.bimeiz.com/jiaoyu/3045.html